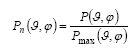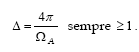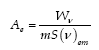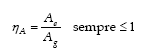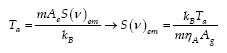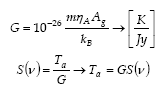2. Parametri descrittivi

Temperatura d’antenna equivalente : T_a

Temperatura a cui dovrebbe trovarsi una resistenza ipotetica per irradiare una potenza di rumore termico  pari a quella ricevuta dall’antenna.

W_ν = potenza per unità di banda [W/Hz]

k_B = costante di Boltzmann

Poiché i flussi osservati sono sempre molto deboli, la temperatura equivalente offre una misura dell’energia emessa dalla sorgente espressa con numeri più maneggevoli.

Beam : P(θ,φ)

E’ anche detto “power pattern” ed è una misura della potenza ricevuta in funzione della distanza angolare dall’asse dello strumento.

Il beam descrive come l’antenna riceve potenza in funzione della direzione, ovvero ne descrive la risposta in ricezione. In analogia con l’astronomia ottica se la radiazione proviene da una sorgente puntiforme il beam rappresenta la PSF (Point Spread Function) dello strumento.

In generale il beam si esprime in coordinate polari e normalizzato al suo valore massimo :

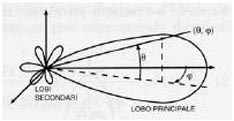
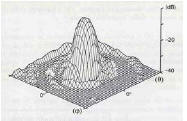
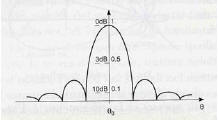
Per rappresentare il beam si utilizza il cosiddetto “diagramma d’antenna”, un grafico 3-D che illustra la P(θ,φ). Nel caso (assai frequente) di simmetria rotazionale è sufficiente una grafico 2-D (v. fig. 2.1) passante per l’asse di simmetria.

Fig. 2.1 : Diagramma d’antenna (da sn : 3-D in coordinate polari, 3-D in coordinate rettangolari, 2-D normalizzato)

I massimi del diagramma prendono il nome di “lobi” : generalmente si distingue un lobo principale (main lobe) seguito da dei lobi minori (lobi secondari, o posteriori).

Half Power Beam Width : HPBW 

Angolo che sottende il livello di metà potenza del lobo principale (-3 dB). Costituisce una buona stima del potere risolutivo dell’antenna.

Beam Width First Nulls : BWFN

Larghezza angolare tra i primi due zeri del diagramma (è circa due volte maggiore della HPBW e più semplice da calcolare).

Angolo solido del diagramma : Ω_A

Integrale del beam esteso all’intera regione in cui esso è diverso da zero :

Per un’antenna isotropa, cioè che riceve allo stesso modo in ogni direzione :

In prima approssimazione il flusso osservato dall’antenna vale :

S(ν)_em= flusso emesso dalla radiosorgente

Direttività : Δ

Esprime la capacità dell’antenna di ricevere gran parte dell’energia da una direzione privilegiata.

Per un antenna molto direttiva Ω_A è molto piccolo. Viene anche indicata come “Guadagno in direttività” oppure come “Guadagno rispetto all’isotropa”

Per un’antenna isotropa :

Angolo solido del lobo principale  : Ω_M

Integrale del beam esteso al solo lobo principale.

Efficienza del lobo principale :  η_M

Fornisce una stima di quanto il diagramma è concentrato nel lobo principale

Area efficace dell’antenna : A_e

Area reale di raccolta dell’antenna, al netto di tutte le perdite subite dal segnale in fase di raccolta e ricezione, ovvero misura globale della capacità di un’antenna di ricevere e riflettere la radiazione.

m = fattore numerico che dipende dalla polarizzazione della radiazione incidente (m= 0.5 se la radiazione incidente è non polarizzata, m=1 se l’antenna riceve tutte le componenti di polarizzazione dell’onda incidente).

In generale l’area efficace dipende dalla direzione di puntamento :

Vale la seguente :

Efficienza dell’apertura : η_A

Misura del discostamento dal caso ideale, nel quale l’assenza di perdite del segnale comporterebbe un’area efficace pari all’area geometrica dell’antenna.

Con le opportune sostituzioni si ottengono le seguenti :

Guadagno dell’antenna : G

E’ un’altra misura della capacità dell’antenna di raccogliere flusso.

A parità di flusso emesso, se si dispone di un alto guadagno si ottiene un’elevata temperatura d’antenna e dunque un’elevata potenza ricevuta, pertanto è più facile rivelare il segnale.

                                                                            Webmaster